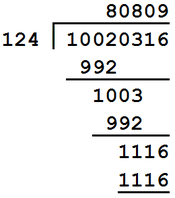Brain Teaser Answers
1. Forty
3. You only need to draw 1 marble. The key to the solution is knowing that all the labels are incorrect. So you just need to draw a marble from the box labeled BW. If the marble is black, you know that the box must contain two black marbles (otherwise the label would be correct). That means the box labeled WW cannot contain the two black marbles, nor can it contain two white marbles (due to its label), so it must contain one black and one white. Lastly, the box labeled BB must contain the two white marbles. You can use the same process of elimination if the marble drawn from the BW box is white.
4. White can avoid checkmating black by moving his rook four squares to the west. This checks the black king, but black may now capture the checking bishop with his rook.
[P.S. It is possible to have the two white bishops on the same color square; a white pawn that travels to the last row can be exchanged for a bishop.]
[P.S. It is possible to have the two white bishops on the same color square; a white pawn that travels to the last row can be exchanged for a bishop.]
5. "In long division, when two digits are brought down instead of one, there must be a zero in the quotient. This occurs twice, so we know at once that the quotient is x080x. When the divisor is multiplied by the quotient's last digit, the product is a four-digit number. The quotient's last digit must therefore be 9, because eight times the divisor is a three-digit number.
"The divisor must be less than 125 because eight times 125 is 1,000, a four-digit number. We now can deduce that the quotient's first digit must be more than 7, for seven times a divisor less than 125 would give a product that would leave more than two digits after it was subtracted from the first four digits in the dividend. This first digit cannot be 9 (which gives a four-digit number when the divisor is multiplied by it), so it must be 8, making the full quotient 80809.
"The divisor must be more than 123 because 80809 times 123 is a seven-digit number and our dividend has eight digits. The only number between 123 and 125 is 124. We can now reconstruct the entire problem as follows:"
"The divisor must be less than 125 because eight times 125 is 1,000, a four-digit number. We now can deduce that the quotient's first digit must be more than 7, for seven times a divisor less than 125 would give a product that would leave more than two digits after it was subtracted from the first four digits in the dividend. This first digit cannot be 9 (which gives a four-digit number when the divisor is multiplied by it), so it must be 8, making the full quotient 80809.
"The divisor must be more than 123 because 80809 times 123 is a seven-digit number and our dividend has eight digits. The only number between 123 and 125 is 124. We can now reconstruct the entire problem as follows:"